Cómo crear modelos de regresión espacial en ArcGIS
- publicado por cursosonlinegis
- Categorías Cursos Online Gis
- Fecha enero 27, 2022
- Comentarios 0 Comentarios
A los detectives de SIG les encanta usar modelos de regresión espacial
El detective de GIS experto en tecnología ama la regresión espacial porque se usa para modelar relaciones espaciales. Los modelos de regresión investigan qué variables explican su ubicación.
Por ejemplo: si tiene ubicaciones de delitos en una ciudad, puede utilizar la regresión espacial para comprender los factores que se encuentran detrás de los patrones delictivos . Podemos usar la regresión espacial para comprender qué variables (ingresos, educación y más) explican la ubicación del crimen.
A continuación, se puede utilizar un modelo de regresión espacial para la toma de decisiones. Por ejemplo, puede responder dónde hay ubicaciones adecuadas para las comisarías. Los modelos de regresión espacial también se utilizan para predecir ubicaciones futuras de delitos e incluso en otras ciudades.
Entendamos algunas de las terminologías en los modelos de regresión.
- Variable dependiente (Y) : ¿Qué está tratando de predecir? (Ubicación de los delitos)
- Variable independiente (X) : Variables explicativas que explican la variable dependiente. (Ingresos, educación, etc.)
- Coeficiente beta : ponderaciones que reflejan la relación entre la variable explicativa y la dependiente.
- Residual : el valor no explicado por el modelo.
Fórmula de regresión :
y = β 0 + (β 1 × x 1 ) + (β 2 × x 2 ) +… + (β n × x n ) + Ε
Análisis de regresión espacial en ArcGIS
Pongamos en acción las herramientas de regresión de ArcGIS mediante la creación de un índice de idoneidad del hábitat (HSI), también conocido como función de selección de recursos (RSF). Con 308 ubicaciones GPS de ciervos de las marismas, investigamos la relación entre los ciervos de las marismas y su paisaje.
Importante tener en cuenta: este es un escenario hipotético con datos inventados.
Respondemos preguntas como:
- ¿Qué recursos seleccionan o evitan los ciervos de las marismas?
- ¿Cuáles son algunos de los factores que contribuyen a la ubicación de los ciervos de las marismas?
¿Por qué crear un HSI?
Un administrador de recursos de la tierra usa HSI para tomar mejores decisiones sobre el paisaje. Si un HSI muestra que los ciervos de los pantanos prefieren los tipos de hábitat de humedales, un administrador de recursos de la tierra puede preservar estos tipos de hábitat. Un administrador de recursos de la tierra puede prohibir el desarrollo de infraestructura porque un HSI muestra la capacidad de un hábitat determinado para soportar ciervos de los pantanos. El HSI se puede extrapolar para predecir los ciervos de los pantanos en otros lugares.
Variables explicativas
¿Cuáles son las variables explicativas del venado de los pantanos? Ésta puede ser la parte más difícil del modelado de regresión. Necesitamos investigar los posibles tipos de hábitat para los ciervos de los pantanos. Aquí es donde el consejo de un experto resulta útil. Esto es lo que encontramos:
Según la literatura, los ciervos de los pantanos seleccionan la vegetación y el agua naturales . Pero, ¿hay características de la tierra que puedan perturbar a los ciervos de los pantanos? Exploramos estas variables independientes utilizando nuestro análisis de regresión espacial.
Variables independientes y dependientes
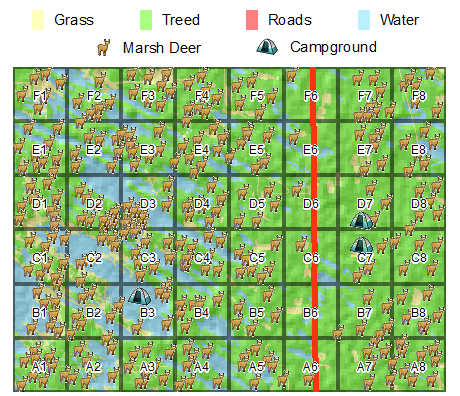
Nuestra zona de estudio se caracteriza por la vegetación natural y el mar abierto. Una carretera atraviesa las celdas A6-F6 que pueden actuar como una perturbación potencial. Los campamentos también están presentes en las celdas B3, C7 y D7.
Distribución de ciervos de los pantanos y campamentos
Cada punto representa la posición GPS de los ciervos de los pantanos. Visualmente, parece haber menos ciervos de los pantanos cerca de las carreteras y los campamentos. Otra observación es que los ciervos de los pantanos aparecen más densos en las celdas D2 y D3 donde hay humedales.
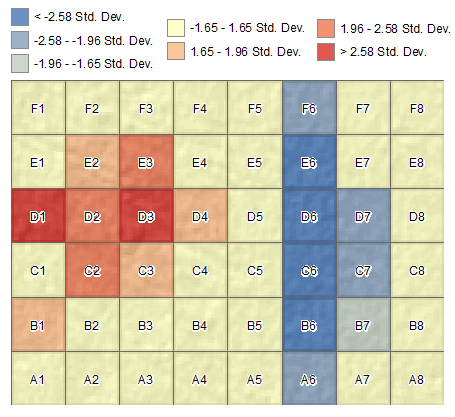
Análisis de hotspot
Este mapa de puntos de acceso confirma menos ciervos cerca de las carreteras en un grado de menos de -2 desviaciones estándar de la media. Los ciervos de los pantanos son más densos cerca de las celdas D2. Aparte de estos dos puntos bajos y calientes, no parece haber más patrones espaciales en el área de estudio.
- ¿Por qué hay tantos ciervos en estos puntos calientes?
- ¿Cuáles son algunos de los factores que contribuyen a estos puntos calientes?
Estos son los tipos de preguntas que pueden responderse mediante el análisis de regresión. Usemos la regresión espacial para modelar las relaciones espaciales entre los ciervos de los pantanos y las características de la tierra.
Regresión de mínimos cuadrados ordinarios (OLS)
El primer paso es agrupar las variables independientes y dependientes por celda de la cuadrícula. No podemos considerar las ubicaciones de los ciervos Marsh como puntos. La tabla debe tener el número de ciervos, campamentos y humedales para cada celda de la cuadrícula. La siguiente tabla es un ejemplo de una tabla preprocesada con OLS.
Usaremos la herramienta “Regresión de mínimos cuadrados ordinarios” en el kit de herramientas “Modelado de relaciones espaciales”.
Modelo de regresión ordinaria de mínimos cuadrados:
Clase de entidad de entrada : Celdas de cuadrícula con datos agregados
ID única : Un campo de ID único (p. Ej., 1, 2, 3 …)
Clase de entidad de salida : Ruta y nombre de la salida
Variable dependiente : Recuento de ciervos
Variables explicativas : Campamentos , carreteras y
archivo de informe de producción de agua : genera un archivo de informe.
Después de ejecutar la herramienta OLS, los residuos del modelo de predicción se agregarán a su pantalla. Los residuales son esencialmente el error en el modelo.
Echemos un vistazo más de cerca a lo que es realmente un residual antes de seguir adelante. Si miramos la celda A1 (abajo a la izquierda), se encontraron 9 ciervos en esta celda de la cuadrícula. El modelo OLS construyó pesos basados en la cantidad de árboles, humedales, césped, caminos y campamentos en la celda. Estos pesos son los valores del coeficiente beta. Cuando se introdujeron los pesos en la fórmula de regresión, se estimó que había 6,98 ciervos en la celda A1. Cuando resta 6,98 de 9, obtenemos un residuo de 2,01. En otras palabras, el modelo subestima el valor real en 2,01.
Valores residuales de regresión de mínimos cuadrados ordinarios:
| Variable | Coeficiente beta | pag | VIF |
| Interceptar | β 0 = 5,916744 | 0,0000001 * | —– |
| Carreteras | β 1 = -0,524393 | 0,0000001 * | 1.150233 |
| Agua | β 2 = 0,056088 | 0,0000001 * | 1.139367 |
| Acampar | β 3 = -3,558805 | 0,0000001 * | 1.010354 |
El bajo coeficiente beta negativo de los campamentos (-3,56) se puede interpretar como áreas donde los ciervos de los pantanos evitan. Las carreteras también tenían un valor negativo de -0,52, lo que significa que los ciervos no seleccionan estas cuadrículas. Los ciervos de los pantanos prefieren los humedales como hábitat adecuado. Este modelo confirma esta creencia.
Podemos insertar manualmente el modelo de coeficiente beta en el modelo de regresión. El resultado es el valor previsto. En nuestro caso, es el número predicho de ciervos en la celda de la cuadrícula.
y = β 0 + (β 1 × x 1 ) + (β 2 × x 2 ) +… + (β n × x n ) + Ε
A1 = 5,916744 + (-0,524393 × 0) + (0,056088 × 30) + (-3,558805 × 0)
A1 = 7,59
Este modelo MCO logra un valor de R cuadrado ajustado de 0,795. Con estos 3 factores, podemos explicar el 79,5% de la variación que se está produciendo.
¿Qué le falta al modelo? Depredadores conocidos, edad del bosque, tipo de humedal: incluyen otras facetas de
Factor de inflación de la varianza (VIF):
Otra estadística de interés es el Factor de Inflación de Varianza (VIF). Si el VIF> 7.5, esto indica redundancia entre las variables explicativas. Nuestro modelo HSI cumplió estos criterios con VIF
Probabilidad y probabilidad robusta:
Un asterisco (*) indica que el coeficiente es estadísticamente significativo (p
Estadística de Jarque-Bera:
Cuando esta prueba es estadísticamente significativa (p
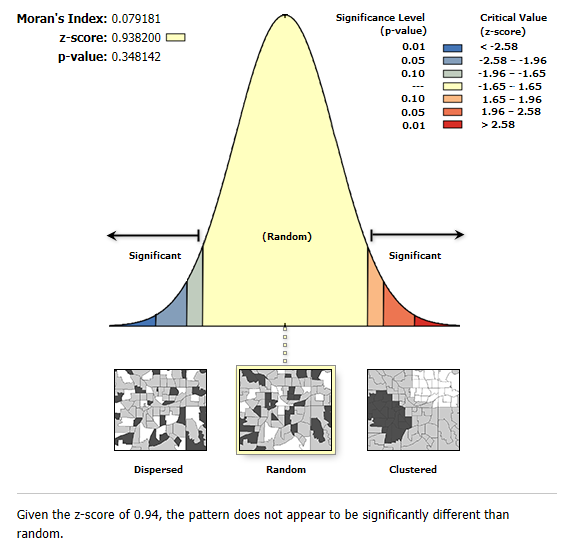
Autocorrelación espacial I de Moran
La autocorrelación espacial nos dirá si las predicciones por debajo / por encima son aleatorias. Ningún modelo puede predecir a la perfección y siempre hará una predicción excesiva o insuficiente. La autocorrelación espacial investiga si el modelo MCO se distribuye aleatoriamente.
Autocorrelación espacial I de Moran:
Clase de entidad de
entrada: Salida OLS Campo de entrada: Residual estándar (StdResid)
Generar informe : SÍ
Al hacer clic en Aceptar, se generará un informe. Haga doble clic en el informe y asegúrese de que los resultados sean aleatorios.
LEER MÁS : Autocorrelación espacial y I de Moran en GIS
¿Caso cerrado?
La herramienta de regresión espacial ArcGIS se utilizó para construir una relación espacial entre los ciervos de los pantanos, los campamentos, las carreteras y los humedales. Las herramientas de regresión investigaron la relación entre estos factores y generaron ponderaciones para cada variable.
Estos pesos se conectaron a la fórmula de regresión para calcular y predecir el número de ciervos. El factor de inflación de la varianza, los puntajes z, el I de Jarque-Bera y Moran aseguraron la robustez y la significancia estadística en el modelo de regresión espacial.
El modelo de regresión muestra cómo los ciervos de los pantanos seleccionan los humedales como hábitat adecuado. También muestra que los ciervos de los pantanos tienden a evitar los campamentos y las carreteras.
Esto es útil para los administradores de recursos de la tierra para restringir potencialmente el desarrollo de campamentos y carreteras para conservar este tipo de ciervos. El modelo de regresión también se puede utilizar para predecir ciervos de los pantanos en otras áreas.
Fuente: gisgeography.com/spatial-regression-models-arcgis/
También te puede interesar
Optimizando el Conteo de Plantas y Árboles con Sistemas de Información Geográfica (SIG)
La gestión eficiente de recursos naturales es esencial para el equilibrio ambiental y la planificación sostenible. En este artículo, exploraremos cómo los Sistemas de Información Geográfica (SIG) y técnicas avanzadas, como Machine Learning, pueden potenciar el conteo de plantas y …
Explorando el Potencial del Deep Learning en ArcGIS Pro
En el vertiginoso mundo de la tecnología geoespacial, el aprendizaje profundo emerge como una fuerza transformadora, permitiendo análisis más avanzados y precisos de datos espaciales. En este artículo, exploraremos qué es el Deep Learning, cómo implementarlo en ArcGIS Pro y …
Descripción e Importancia de un Curso de Arcgis Pro
Descripción de Arcgis Pro ArcGIS Pro es un software de SIG (Sistema de Información Geográfica) desarrollado por Esri, una compañía líder en el campo de los SIG. Es una aplicación de escritorio de SIG potente y avanzada que se utiliza …